４—５岁幼儿数数行为的规则性与策略化应用特点的研究

 

【内容提要】 本研究的主要目的是考察 4 — 5 岁儿童数数行为的规则性和策略化应用特点。研究选取了 104 名幼儿园中班儿童（年龄范围 4 — 5 岁）， 男女各半，采用现场实验法进行了逐一测查，测查任务为标准计数任务和数字复制任务。结果发现： 4 — 5 岁儿童的数数行为已经遵循一些数数规则，如固定顺序原则、一一对应原则和基数原则；但该年龄段的儿童还不会自发地把数数作为问题解决的策略应用于比较两组物体数目的问题上。

【英文摘要】 104 young children from three kindergartens middle 　 classeswere tested 　 for 　 their 　 counting 　 competence. 　 We 　 used 　 thestandard 　 counting 　 task 　 to 　 test 　 childrens 　 principledunderstanding of counting. As Gelman 　 and 　 Gall istel 　 (1978 )have found, we deduced the stable - order principle, the 　 one- to - one principle and the cardinality principle in 　 Chinesechildrens countin g. And we also found that 4 - and 5 - 　 year-old children cant apply counting to solve simple 　 arithmeticproblems in number reproduction task.

【关 键 词】 数数 / 固定顺序原则 / 一一对应原则 / 基数原则 / 策略化应用

    counting/stable-order principle/one to one correspondence/cardinality

1 　问题提出

    幼儿的数数能力是儿童早期数学能力的重要组成部分，是幼儿一项重要的认知能力。格尔曼等人 [1] 指出， 数数是幼儿用于建构非正式数学知识系统的重要工具。 非正式数学知识（ informal 　 mathematicalknowledge ）是指儿童依靠实物和对实物的表象获得的数学知识。 皮亚杰认为，　　儿童在获得正式的数学知识（ formal 　　　 mathematicalknowledge ，即使用抽象 数学概念 的能力， 如书写数字和数学运算符号）之前已经具有了一些数学认知能力，如小数目的数数、确定两组物体之间的数量关系等等。数数能力是儿童较早获得的数学能力，随着年龄的增长，儿童把数数能力与其它数学知识相结合，能够逐步创造出计数策略，进而建构其非正式的数学知识系统。对于幼儿数数行为的本质特征问题，心理学界基本有两种看法：桑代克认为“数数是无意义联结的集合”，皮亚杰也认为幼儿的数数只是一种机械的重复行为；而格尔曼 [1] 等人认为幼儿的数数行为具有一些概念性的特征， 如幼儿的数数是以一些重要的数学原则，如一一对应等原则为基础的。

    儿童数学能力的发展是国内发展心理学较早的研究课题之一。 60 年代初，沈家鲜对 3 — 4 岁儿童数概念形成做了初步研究； 70 年代末、 80 年代初至今，关于儿童数概念和运算能力发展的研究大量出现 [2,3,4] ，积累了较多的相关资料。这些研究或考察不同年龄段儿童数数能力发展的情况，或从不同任务水平角度对儿童的数数能力进行研究。这些任务水平包括口头数数、按物说数和按数取物等等。然而国内学者对于幼儿数数行为特征问题的专门探讨还较少，而幼儿的数数行为是否遵循了一定的规则、幼儿对这些规则的理解和掌握程度以及幼儿是否能自发将数数作为解决数学问题的策略来使用，能够在一定程度上反映出儿童认知发展的水平。因此本研究试图通过观察 4 — 5 岁幼儿的数数，考察其数数行为是否遵循一定的规则，以及他们是否能够将数数作为一种问题解决策略来使用，从而了解我国 4 — 5 岁幼儿认知能力的实际发展水平。

2 　研究方法

    2.1 　被试：随机选取北京市区三所幼儿园的中班幼儿 104 名，年龄范围为 4 — 5 岁，男女比例大致相当。在北师大幼儿园、蓟门里幼儿园和果子市幼儿园选取的中班幼儿中， 4 岁组（ 3 岁 7 个月至 4 岁 6 个月）幼儿人数分别为 14 人（男 7 人，女 7 人）， 4 人（男 1 人，女 3 人）和 12 人（男 6 人，女 6 人），共 30 人（男 14 人，女 16 人）； 5 岁组（ 4 岁 7 个月至 5 岁 6 个月）幼儿人数分别为 26 人（男 16 人，女 10 人）， 26 人（男 14 人， 女 12 人）和 22 人（男 10 人，女 12 人），共 74 人（男 40 人，女 34 人）。

    2.2 　研究工具和测试过程

    　本研究采用“儿童数学能力测查”（ Alice 　 Klein ， PrenticeStarkey & Ann Wakeley ， 1997 ）中的“标准计数任务”来测查幼儿的数数能力，以其中的“数字复制任务”测查儿童数数策略的使用情况。

    测查在幼儿园中一个相对安静的房间里进行，为个别施测，由一名经过培训的、有幼教经历的人担任主试。

    标准计数任务要求幼儿数一数并说出粘在硬纸板上的、以水平方向放置的一排物体的总数，该项任务总共包括 4 项小任务， 物体总数分别为 3 个， 7 个， 15 个和 30 个。

    数字复制任务的简要测查过程是这样的：主试在儿童面前放好两个小玩具：玩具 1 和玩具 2 ；在儿童身后约 1 米远的另一张桌子上放两个盘子，分别盛有水果形状的橡皮。主试在玩具 1 前放置一些水果橡皮作为范例（ 3 个草莓或 9 个香蕉），要求幼儿从身后的盘子里取一样多的水果橡皮（草莓或香蕉）放在玩具 2 面前。

3 　结果及分析

    　　 3.1 　幼儿在标准计数任务上的表现

    通过对幼儿在标准计数任务上的表现进行编码和分析，我们发现随着物体总数的增加，儿童数数的正确率逐渐下降，具体结果见下表。

    　　表 1 　　　　幼儿在标准计数任务上的通过率

 

任务水平　 4 岁组通过人数 ( 人 ) 　 5 岁组通过人数 ( 人 ) 　百分比差异检验

　　及通过率 (%) 　　　　及通过率 (%) 　　　　 X[2](P 值 )

3 个物体　　 29(96.7) 　　　　　　 73(98.6) 　　　　　 2.78(.598)

7 个物体　　 27(90.0) 　　　　　　 64(86.5) 　　　　　 0.33(.541)

15 个物体　　 24(80.0) 　　　　　　 54(73.0) 　　　　　 0.57(.632)

30 个物体　　 16(53.3) 　　　　　　 40(54.1) 　　　　　 0.68(.834)

 

   

    在进行测查前我们了解到三个幼儿园中班算术课的进度大致相同，所有的幼儿都已学习了 1 — 20 的数数和 1 — 10 个物体的点数。通过表 1 可见， 4 — 5 岁幼儿的数数能力尚处于发展阶段，还未达到较高的水平。

    格尔曼等人认为幼儿数数时遵循一些规则，本研究通过观察和分析我国幼儿数数时的行为表现，发现我国 4 — 5 岁幼儿的数数行为也遵循以下几条规则：

    3.1.1 　幼儿的数数行为遵循一一对应的计数规则。

    对于 3 个物体，幼儿能够不用数而直接看出物体的总数是 3 。在点数 7 个、 15 个及 30 个物体时， 4 岁组和 5 岁组 90 ％以上的幼儿在数数的时候，都是用手指挨个指着物体，按从左至右或从右至左的顺序，出声或不出声地一一点数，他们已经知道数数时一个物体只和一个数字相对应，这说明他们的数数是以一一对应规则为基础的。

    极少数幼儿可以不借助手的动作而直接一边看一边数，这些幼儿数数时虽然没有借助手去指物体，但从其数一个数字点一下头的动作可以看出他们的数数也是遵循一一对应规则的。

    3.1.2 　幼儿的数数行为遵循固定顺序的计数规则。

    幼儿在点数 7 个、 15 个及 30 个物体时， 从他们出声的数数行为中可以发现，几乎所有 4 岁组和 5 岁组幼儿都知道按照一种固定的顺序来数数，即按“ 1 ， 2 ， 3 ， 4 ， 5 ，……”的顺序来数数， 说明他们的数数遵循固定顺序的规则。

    3.1.3 　幼儿的数数行为遵循基数规则。

    基数规则指数数时数到的最后一个数代表这组物体的总数。本研究中的幼儿在数完一组物体后，几乎所有 4 岁组和 5 岁组幼儿都能够立即把数到的最后一个数作为这组物体的总数报告出来，说明他们了解了基数规则，他们的数数是以基数规则为基础的。

    上述结果说明 4 — 5 岁幼儿的数数行为已经遵循了一定的规则。

    　　 3.2 　幼儿在数字复制任务上的表现

    通过分析幼儿在数字复制任务上的表现，可以清楚地看到幼儿使用数数策略解决简单数学问题的情况：

    3.2.1 　在 3 个物体的数字复制任务上，幼儿采用不一一点数数而直接感知物体总数的方法， 98 ％的幼儿都正确完成了 3 个物体的数字复制任务。

    3.2.2 　在 9 个物体的数字复制任务上，复制前点数了源系列（注：源系列：指主试摆出的物体系列）物体数目的幼儿， 4 岁组有 14 人， 占本年龄组人数的 46.7 ％； 5 岁组有 40 人，占本年龄组人数的 54.1 ％， 这说明一半的幼儿是理解该项任务的要求的。然而，幼儿虽然点数了源系列物体的数量，但他们中大部分人仍得不出正确的答案，显然他们还不知道如何使用数数策略来解决此类问题（见图 1

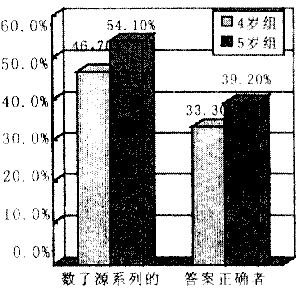    图 1 　 9 个物体的数字复制任务完成情况

    4 岁组的幼儿复制完成后使用明显数数策略（指可被主试观察到的数数行为）以查对两组物体数目的只有 5 人，占本年龄组幼儿数的 16. 7 ％； 5 岁组的幼儿复制完成后使用明显数数策略以查对两组物体数目的有 10 人，占本年龄组幼儿数的 13.5 ％，人数比例略低于 4 岁组儿童， 原因可能在于我们考察的是明显的数数行为，而 5 岁组幼儿由于数数技能更熟练，更多采用默数的行为，因此明显的数数行为有所减少。以上结果说明大部分 4 — 5 岁的幼儿还不知道使用数数策略来解决两组物体数目是否相等的问题；此外通过百分比差异检验发现两组儿童中复制完成后使用明显数数策略的人数百分比没有显著差异，说明 5 岁组幼儿与 4 岁组幼儿在数数策略使用上处于相似的发展水平（表 2 ）。

    周燕　庞丽娟　赵红利： 4 — 5 岁幼儿数数行为的规则性与策略化应用特点的研究

    表 2 　　　　 9 个物体的数字复制任务上儿童使用数数策略的情况

 

　　　复制前点数源系列　　　　复制完成后使用

　　　儿童的人数 ( 人 ) 及　　　　数数策略的人数

　　　百分比 (%) 　　　　　　　 ( 人 ) 及百分比 (%)

4 岁组　　　　　　　　 14(46.7) 　　　　　　 5(16.7)

5 岁组　　　　　　　　 40(54.1) 　　　　　　 10(13.5)

两组百分比差异　　　 x[2]=0.427(P=.524) 　 x[2]=0.533(P=.561)

 

   

    全体幼儿中，使用了明显的数数策略以查对两组物体数量并得出正确结果的只有 7 人；当幼儿在玩具 2 前放好水果橡皮后，主试询问两组物体数目是否一样时，只有 2 名幼儿（ 1.9 ％）数了两组物体的数目之后回答“是一样的”，大部分幼儿不数任何一组物体的数目而立刻回答“是一样的”。另外，两个年龄组中， 5 岁组不通过明显的数数策略而得出正确答案人数比例高于 4 岁组。

    表 3 　　　　　部分幼儿数字复制任务完成情况

 

在 9 个物体的数字　　　　　人数 ( 人 ) 及百分比 (%)

复制任务中的表现

能正确数出 15 个物　　复制前明显数源系列　　　　　　 12(22.2)

体的幼儿 ( 共 54 人 ) 　　未使用明显策略而正确完成　　　 27(50.0)

能正确数出 30 个物　　复制前明显数源系列　　　　　　 12(30.0)

体的幼儿 ( 共 40 人 ) 　　未使用明显策略而正确完成　　　 24(60.0)

 

   

    由表 3 可见，虽然幼儿的数数能力已经发展到一定水平， 能够正确数出 15 个或 30 个物体的数量，但他们还不能将数数作为解决问题的策略来灵活使用，不能将其用于解决 9 个物体的数字复制任务。 同时也可看出，与能正确数出 15 个物体的幼儿相比，能正确数出 30 个物体的幼儿，其复制前明显数源系列物体和能正确完成 9 个物体复制的人数比例较高，说明他们的数数策略使用能力和完成复制任务的能力都较高，同时说明了幼儿的数数能力和物体复制能力的发展是相互促进的。

    如果不考虑幼儿完成任务的正确性，只考察幼儿是否自发地使用明显的数数策略来解决问题，我们发现大部分幼儿还不能将数数作为策略来解决两组物体数目是否相等的问题（见表 2 和表 3 ）。

4 　讨论

    　　 4.1 　关于幼儿数数行为的规则性特点。

    本研究的结果表明， 4 — 5 岁幼儿数数时已经能够遵循一些数学规则。我们认为，幼儿的这种能力不能简单地将其视为模仿性或技能性的，因为任务有各种情境，而成人不可能穷尽各种情境对幼儿进行模仿训练。幼儿在刚开始数数时（ 2 — 3 岁），可能更多的是在模仿成人的行为，但随着幼儿动作水平和认知能力的发展，他们的数数行为就是以理解数数规则为基础的了。例如在本研究中，在完成标准计数任务时，许多幼儿没有借助手的动作而默数并得出了正确的答案，这些幼儿的表现单用“模仿”是很难解释的，因为这种内部数数行为需要更多地依赖对数数规则的理解。我们认为，幼儿期是先天性的数能力和后天的数数技能相互促进、同时发展的时期，先天性的数能力调节着数数技能的发展，同时数数技能的发展也促进了先天数能力的展现。幼儿数数行为的规则性可能就是在先天的一些数能力和后天数数技能发展的相互作用下形成的。 4 — 5 岁幼儿是在理解的基础上运用一些重要数数规则进行计数活动的。

    一些研究者认为 ，幼儿在数数时表现出遵循一定的规则， 并不能说明幼儿已经理解和掌握了这些数数规则，幼儿可能只是在模仿成人的数数行为，因此这只能被看作是幼儿的一种数数技能。格尔曼等人 认为数数规则先天性地存在于儿童的头脑中， 它调节着外部环境和儿童数数技能发展之间的相互作用。但是，由于幼儿的数数技能和理解力还处于较低水平，因此他们还不知道如何以及在何时使用这些数数规则。例如，在点数物体时，随着物体数目的增加，幼儿数数的正确性逐渐下降，幼儿易犯一些错数（数词顺序上的错误）、漏数或重复数的错误。格尔曼等人用检查错误任务对幼儿的数数行为做了进一步的研究。研究是这样进行的：主试暗中操纵一个小木偶去数数， 3 — 5 岁的幼儿在一旁观察，幼儿的任务是判断木偶的数数是否正确。主试安排小木偶有时数得对，有时犯一些幼儿常犯的错误。结果发现幼儿能够迅速地将正确的判断为正确，也能发现违反数数规则所犯的错误。这个结果证明了幼儿很早就已经掌握了基本的数数规则。格尔曼等人提出的先天性的数数规则共有 5 条，除了本研究中提到的 3 条关于如何数的规则外，还包括 2 条允许性原则，即哪些事物可被点数。

    　　 4.2 　关于幼儿数数行为的策略化应用特点。

    与理解水平相比，应用是认知发展的更高水平。我们发现， 虽然 4 — 5 岁幼儿的数数能力已经发展到一定水平， 而且他们也能理解数字复制任务的要求，但能够运用最直接有效的策略——数数，来解决问题的幼儿人数比例非常低。本研究中 9 个物体的复制任务难度较高：主试没有明确地说出物体的数量，也没有要求幼儿数物体的数目，主试只简单地问两组物体是否一样多，因此此项任务实际考察了幼儿多个方面的数学能力，包括按物点数的能力、按数取物的能力以及比较两组物体数目是否相等的能力等。在进行按物点数时，由于物体的摆放是无规则的，加大了点数的难度，幼儿必须记住哪些物体数过了，哪些还没有数。在进行按数取物时幼儿要口手一致地完成这个步骤，对幼儿动作的协调性和精确性也提出了一定的要求。 4 — 5 岁幼儿的精细动作发展水平有限，这可能也是造成幼儿成功率低的原因之一。此外，由于比较两组物体数目差异任务，与比较一组物体数目变化任务相比，难度更大， 大部分 4 — 5 岁儿童不知道将要比较的两组物体的数目进行逐一点数， 说明儿童的认知水平还处于较低水平，还不会自发地将数数作为问题解决策略应用于两组物体数目的比较上。

    国外的研究发现， 3 — 4 岁幼儿在解决加法和减法问题时，不会自发地使用数数策略 。有研究者认为， 4 岁幼儿开始自发地将数数策略用于解决单系列物体的简单加减法问题上 。但是只有满足下述条件时， 4 岁幼儿才能自发地使用数数策略：被点数过的原始系列被遮盖或数目被改变；问题以口头形式呈现，而不以实物形式呈现 。与单系列物体的加减法不同的是，本研究的数字复制任务考察了幼儿比较两系列物体数目的能力，但研究所得出的结果与国外研究的结果是一致的：虽然 4 — 5 岁的幼儿学会数数已经有一段时间了，而且他们也能够理解数数的一些重要规则，但是他们还不能将数数应用于数学问题的解决中。 4 — 5 岁幼儿数认知能力还要经过一段时间的发展，才能达到更高的水平。

5 　结论

    （ 1 ） 4 — 5 岁幼儿在数数时遵循一一对应、 固定顺序和基数等规则，并且他们是在理解的基础上应用这些规则的。

    （ 2 ） 4 — 5 岁幼儿还不能自发地将数数作为一种策略来解决两组问题数目是否相等的问题。

    （ 3 ）在数数策略的使用方面， 4 岁组和 5 岁组幼儿处于数认知发展的相似水平。

 

 

手工材料